Vectorrekening in vlak en ruimte: Vectoren in vlak en ruimte
 Scalaire vermenigvuldiging
Scalaire vermenigvuldiging
Scalairen
We noteren met \(\lambda \cdot\vec{v}\) de vector die uit de vector #\vec{v}# ontstaat door deze vanuit zijn beginpunt met een getal #\lambda# te vermenigvuldigen, met dien verstande dat we de richting van de vector #\vec{v}# eerst omkeren als #\lambda \lt 0#.
Met andere woorden: \(\lambda \cdot\vec{v}\) is de vector waarvan
- de lengte #\left|\lambda\right|# maal de lengte van #\vec{v}# is en
- de richting gelijk aan die van #\vec{v}# is als #\lambda\gt0# en gelijk aan die van #-\vec{v}# als #\lambda\lt0#.
We noemen #\lambda \cdot\vec{v}# een scalair veelvoud van #\vec{v}# of kortweg veelvoud van #\vec{v}#. Het (schalings)getal #\lambda# waarmee we de vector vermenigvuldigen noemen we een scalar (meervoud: scalairen). Doorgaans schrijven we
- #\vec{v}# in plaats van #1\cdot\vec{v}#,
- #-\vec{v}# in plaats van #(-1)\cdot\vec{v}#,
- #-3\cdot \vec{v}# in plaats van #(-3)\cdot\vec{v}#, enzovoort.
De vector #-\vec{v}# heet wel de tegengestelde van #\vec{v}#.
In de figuur hieronder zijn de vector #\vec{v}# en enkele scalaire veelvouden, alle geplaatst in de oorsprong, geportretteerd.
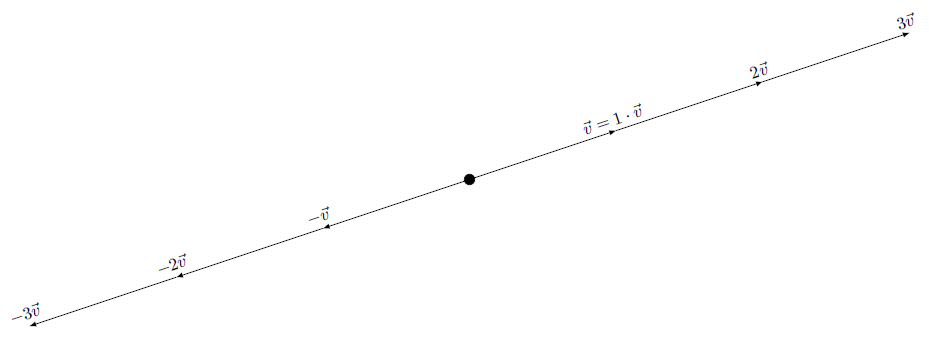
Soms wordt de vermenigvuldigingspunt in de scalaire vermenigvuldiging weggelaten, zoals in #3 \vec{v}# of #3\rv{-7,9}#, maar we streven ernaar de punt in het algemeen goed te laten uitkomen. We zetten de scalar altijd links van de vector.
Scalaire vermenigvuldiging in coördinaten
Voor #\vec{v}# in #\mathbb{R}^2# wordt de scalaire vermenigvuldiging met #r# gegeven door
\[ r\cdot\rv{x,y}=\rv{r\cdot x,r\cdot y}\tiny.\]
Voor #\vec{v}# in #\mathbb{R}^3# wordt de scalaire vermenigvuldiging met #r# gegeven door
\[ r\cdot\rv{x,y,z}=\rv{r\cdot x,r\cdot y,r\cdot z}\tiny.\]
We behandelen het geval #{\mathbb R}^2#. Het bewijs voor #\mathbb{R}^3#, de ruimte, loopt niet wezenlijk anders.
We moeten laten zien dat # \rv{r\cdot x,r\cdot y}# samenvalt met #r\cdot\vec{v}#. Als #r=0#, dan is #\rv {r\cdot x,r\cdot y}=\rv{0,0}=\vec{0}#. Anderzijds is #0\cdot\vec{v}# ook gelijk aan #0\cdot \vec{v}#, want de lengte van #0\cdot \vec{v}# is gelijk aan #0# en #\vec{0}# is de enige vector met lengte gelijk aan #0#.
Voor de rest van het bewijs kunnen we aannemen dat #r\ne0#. Om te kunnen concluderen dat # \rv{r\cdot x,r\cdot y}# en #r\cdot\vec{v}# samenvallen, is het voldoende vast te stellen dat beide vectoren dezelfde lengte en richting hebben.
- De lengte van # \rv{r\cdot x,r\cdot y}# is gelijk aan \[\sqrt{(r\cdot x)^2+(r\cdot y)^2}=|r|\cdot \sqrt{x^2+y^2}\tiny,\]dus #|r|# maal de lengte van #v#. Dit is de lengte van #r\cdot\vec{v}#.
- We onderscheiden twee gevallen.
- Als #r\gt 0#, dan is de richting van # \rv{r\cdot x,r\cdot y}# gelijk aan die van #\rv{x,y}#.
- Als #r\lt0#, dan is de richting gelijk aan die van #\rv{-x,-y}#, de richting van de vector die als representant het lijnstuk heeft dat in de oorsprong begint en in #\rv{-x,-y}# eindigt, en dus ook als representant het lijnstuk heeft dat in #\rv{x,y}# begint en in de oorsprong eindigt; dit is de richting van #-\vec{v}# en dus ook van #r\cdot\vec{v}#.
In beide gevallen is de richting van # \rv{r\cdot x,r\cdot y}# dus gelijk aan die van #r\cdot \vec{v}#.
Rekenregels voor scalaire vermenigvuldiging
Voor de scalaire vermenigvuldiging gelden de volgende rekenregels, waarbij #\vec{v}# een vector en #\lambda#, #\mu# scalairen zijn.
- #0\cdot \vec{v} = \vec{0}#
- #\lambda\cdot\vec{0}=\vec{0}#
- #\lambda\cdot (\mu\cdot \vec{v}) = (\lambda \cdot\mu) \cdot\vec{v}#
- #-\left(\mu\cdot\vec{v}\right)=\left(-\mu\right)\cdot\vec{v}#
De derde regel in woorden: als je de vector #\vec{v}# eerst met #\mu# vermenigvuldigt en het resultaat vervolgens met #\lambda#, dan is het resultaat gelijk aan de vector die je verkrijgt door #\vec{v}# met het product #\lambda\cdot\mu# te vermenigvuldigen.
De eerste regel is hierboven al afgeleid: #0\cdot \vec{v}# heeft lengte #0# en #\vec{0}# is de enige vector met die eigenschap.
De tweede regel volgt ook uit de observatie dat #\vec{0}# de enige vector ter lengte #0# is.
De derde regel volgt onmiddellijk uit de eerste als #\lambda# of #\mu# gelijk is aan #0#, want dan zijn beide zijden gelijk aan #\vec{0}#. Als dit niet het geval is, dan kunnen we de gelijkheid afleiden door vast te stellen dat links en rechts van de gelijkheid vectoren staan met dezelfde richting en lengte.
- De richting kan bij vermenigvuldiging alleen omslaan als het teken van de scalar negatief is. Omdat de scalairen links en rechts even vaak voorkomen, zijn de richtingen links en rechts gelijk.
- De lengte van de vector links is #|\lambda|\cdot |\mu|# maal de lengte van #\vec{v}#. Maar dat is rechts ook het geval. De lengtes van #\lambda\cdot (\mu\cdot \vec{v})# en # (\lambda \cdot\mu) \cdot\vec{v}# zijn dus ook gelijk.
De vierde regel volgt uit de derde met #\lambda = -1#:
\[-\left(\mu\cdot\vec{v}\right) = (-1)\cdot \left(\mu\cdot\vec{v}\right) =\left((-1)\cdot \mu\right)\cdot\vec{v}=\left(-\mu\right)\cdot\vec{v}\tiny.\]
De scalaire vermenigvuldiging in coördinaten geeft\[\begin{array}{rcl}-4\cdot\rv{-4,-2,-5}&=&\rv{-4\cdot -4, -4 \cdot -2, -4\cdot -5}\\
&=&\left[ 16 , 8 , 20 \right]\end{array}\]In de figuur hieronder is #\vec{v}# het zwart getekende lijnstuk van de oorsprong naar #A# en #r\cdot \vec{v}# het rood getekende lijnstuk van de oorsprong naar #B#.


omptest.org als je een OMPT examen moet maken.



