Vector calculus in plane and space: Vectors in Planes and Space
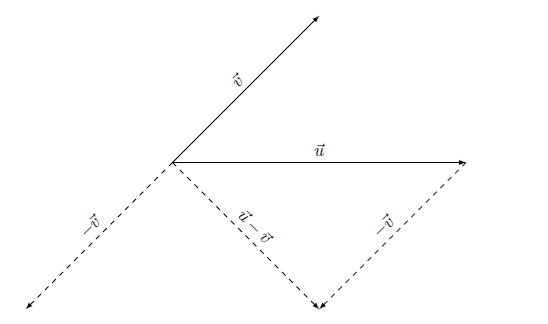
 Addition of vectors
Addition of vectors
The sum of two vectors
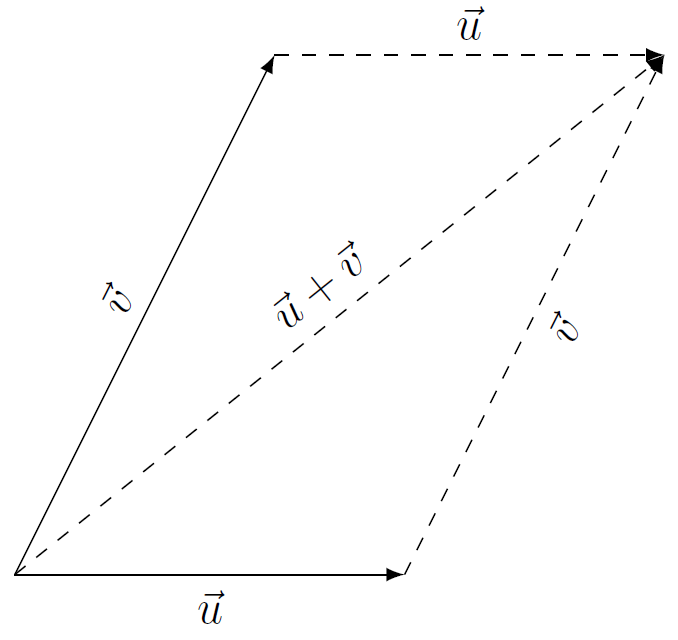
If #\vec{u}# and #\vec{v}# are two vectors with the same starting point (which you can always ensure through repositioning), then #\vec{u}+\vec{v}# is the vector with the same starting point, and the end point is the fourth point of the parallelogram of which #\vec{u}# and #\vec{v}# are two sides. See the figure below.
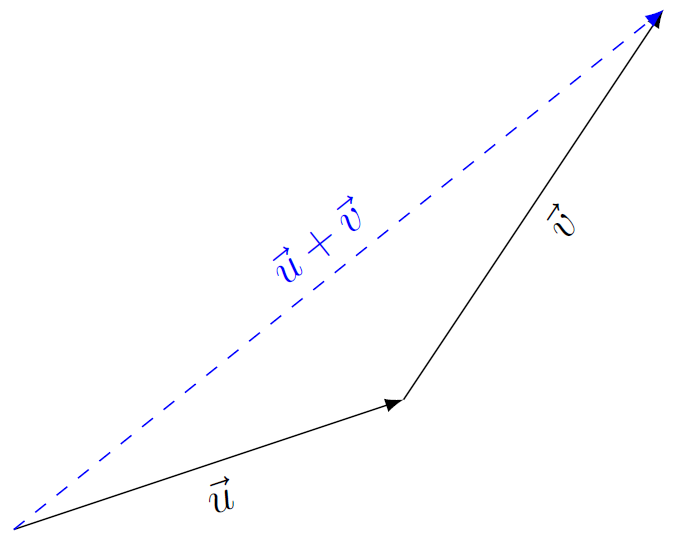
The sum of two vectors #\vec{u}# and #\vec{v}# can also be determined by placing #\vec{u}# and #\vec{v}# head-to-tail, as shown in the figure below:
Instead of #\vec{v}+-\vec{w}#, we usually write #\vec{v}-\vec{w}#. This expression is called the difference of #\vec{v}# and #\vec{w}#.
The addition of vectors can be expressed in terms of coordinates.
Addition of vectors in coordinates
The addition of vectors in coordinates works coordinatewise. This means, that, if #x#, #y#, #z#, #u#, #v#, #w# are real numbers, then
- in #\mathbb{R}^2#: #\rv{x,y}+\rv{u,v}=\rv{x+u,y+v}#
- in #\mathbb{R}^3#: #\rv{x,y,z}+\rv{u,v,w}=\rv{x+u,y+v,z+w}#
Here are the relevant calculation rules for adding vectors.
Calculation rules for the addition of vectors
The addition of vectors satisfies the following rules, where #\vec{u}#, #\vec{v}#, and #\vec{w}# are vectors.
- Associativity: #(\vec{u}+\vec{v})+\vec{w}= \vec{u}+(\vec{v}+\vec{w})# for all vectors #\vec{u}#, #\vec{v}# and #\vec{w}#
- Commutativity: #\vec{v} + \vec{w} = \vec{w}+\vec{v}# for all vectors #\vec{v}# and #\vec{w}#
- Zero vector: #\vec{u} + \vec{0} = \vec{u}#
- Opposing: #\vec{v} + -\vec{v}= \vec{0}# (we then simply write #\vec{v}-\vec{v}=\vec{0}#)
There are also rules of calculation in which both scalar multiplication and addition play a role.
Calculation rules for scalar multiplication and addition of vectors
The scalar multiplication has the following distributivity rules.
- Distributivity of the scalar multiplication of the vector addition: #\lambda\cdot (\vec{v}+\vec{w}) = \lambda \cdot\vec{v} + \lambda \cdot\vec{w}# for all vectors #\vec{v}#, #\vec{w}# and for all scalars #\lambda#.
- Distributivity of the scalar multiplication of the scalar addition: #(\lambda +\mu )\cdot\vec{v} = \lambda \cdot\vec{v}+\mu \cdot\vec{v}# for all scalars #\lambda#, #\mu# and all vectors #\vec{v}#.
By use of subtraction we can describe each vector in plane and space in terms of coördinates.
Vectors in coordinates
If #P# and #Q# are points of #\mathbb{R}^3# (or of #\mathbb{R}^2#), then the vector #\vec{PQ}# coincides with the vector from the origin to the point #Q-P#. In terms of vectors: \[\vec{PQ}=\vec{OQ}-\vec{OP}\]
Every coordinate of the sum #\vec{v}+\vec{w}# is the sum of the same coordinates of #\vec{v}# and #\vec{w}#:
\[\begin{array}{rclcl}\vec{v}+\vec{w}&=&\rv{26,15,6}+\rv{-14,-1,-7}&\phantom{x}&\color{blue}{\text{definitions }\vec{v}, \vec{w}}\\ &=&\rv{26-14,15-1,6-7}&\phantom{x}&\color{blue}{\text{sum per coordinate}}\\&=&\rv{12,14,-1}&\phantom{x}&\color{blue}{\text{simplified}}\end{array}\]
In the following figure the vector sum is drawn by means of a dotted arrow. The representative of the vector #\vec{v}# with origin #\vec{w}# and the representative of the vector #\vec{w}# with origin #\vec{v}# are dotted in blue.

Or visit omptest.org if jou are taking an OMPT exam.