Optelling van vectoren

Vectorrekening in vlak en ruimte: Vectoren in vlak en ruimte

Optelling van vectoren

De som van twee vectoren

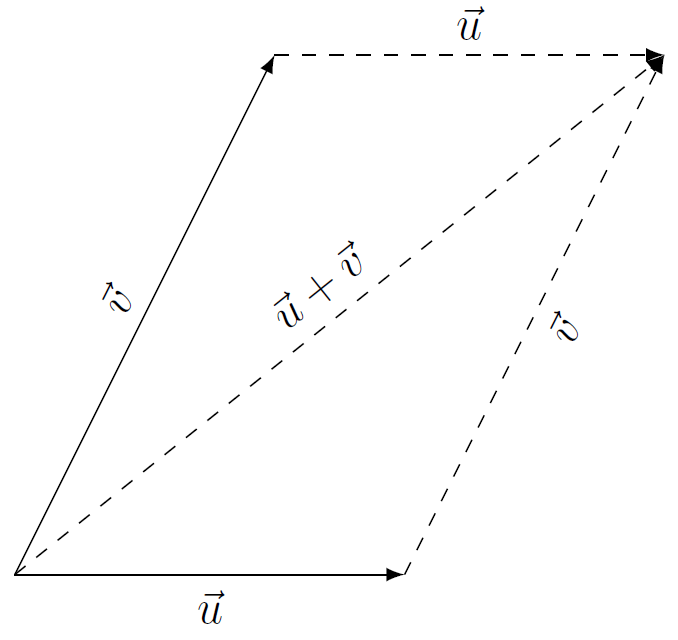
Als #\vec{u}# en #\vec{v}# twee vectoren zijn met hetzelfde beginpunt (daar kun je door verplaatsing altijd voor zorgen), dan is #\vec{u}+\vec{v}# de vector met hetzelfde beginpunt en met als eindpunt het vierde punt van het parallellogram waarvan twee zijden worden gevormd door #\vec{u}# en #\vec{v}#. Zie onderstaande figuur.

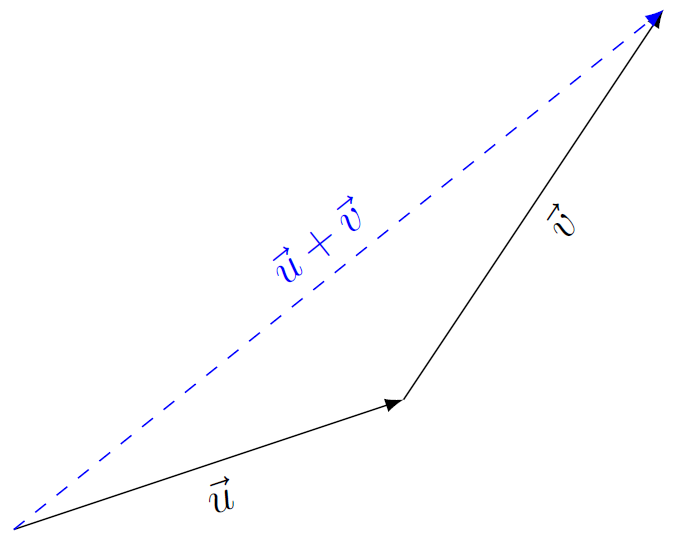
De som van twee vectoren #\vec{u}# en #\vec{v}# is ook te bepalen door #\vec{u}# en #\vec{v}# kop aan staart te leggen, zoals aangegeven in onderstaande figuur:

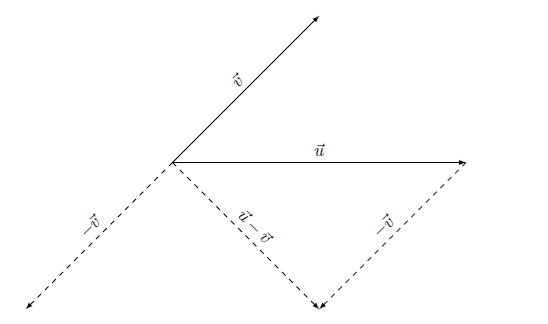
In plaats van #\vec{v}+-\vec{w}# schrijven we doorgaans #\vec{v}-\vec{w}#. Deze uitdrukking wordt het verschil van #\vec{v}# en #\vec{w}# genoemd.

Aftrekken

Trekken we #\vec{v}# van #\vec{u}# af, dan vinden we het verschil #\vec{u}-\vec{v}#. Zie onderstaande figuur.

Eerst #\vec{v}# bij #\vec{u}# optellen en dan #\vec{v}# aftrekken, levert weer #\vec{u}# op. Dit is te danken aan de hieronder beschreven associativiteit.

De nulvector

Voor elke vector #\vec{u}# geldt #\vec{u} + \vec{0} = \vec{u}#.

Optellen van een vector #\vec{v}# en zijn tegengestelde #-\vec{v}# levert de nulvector:
\[\vec{v}-\vec{v}=\vec{0}\]

We kunnen de optelling van vectoren uitdrukken in coördinaten.

Optelling van vectoren in coördinaten
De optelling van coördinaatvectoren vindt coördinaatsgewijs plaats. Dat wil zeggen, als #x#, #y#, #z#, #u#, #v#, #w# reële getallen zijn, dan geldt

in #\mathbb{R}^2#: #\rv{x,y}+\rv{u,v}=\rv{x+u,y+v}#
in #\mathbb{R}^3#: #\rv{x,y,z}+\rv{u,v,w}=\rv{x+u,y+v,z+w}#

Deze uitspraken volgen uit het feit dat de rechter leden precies de vierde punten zijn van het parallellogram met als hoekpunten de oorsprong en de twee coördinaatvectoren in het linker lid.

Hier volgen de voor ons relevante rekenregels voor de optelling van vectoren.

Rekenregels voor de optelling van vectoren

De optelling van vectoren voldoet aan de volgende regels, waarbij #\vec{u}#, #\vec{v}# en #\vec{w}# vectoren zijn.

Associativiteit: #(\vec{u}+\vec{v})+\vec{w}= \vec{u}+(\vec{v}+\vec{w})# voor alle vectoren #\vec{u}#, #\vec{v}# en #\vec{w}#
Commutativiteit: #\vec{v} + \vec{w} = \vec{w}+\vec{v}# voor alle vectoren #\vec{v}# en #\vec{w}#
Nulvector: #\vec{u} + \vec{0} = \vec{u}#
Tegengestelde: #\vec{v} + -\vec{v}= \vec{0}# (we schrijven dan kortweg #\vec{v}-\vec{v}=\vec{0}#)

Associativiteit

De associativiteit van de optelling is een rekenregel waarvan de betekenis misschien niet meteen duidelijk is, omdat associativiteit bijna vanzelfsprekend lijkt. Optelling van vectoren is tot nut toe alleen beschreven voor twee vectoren.

Maar wil je bijvoorbeeld drie vectoren optellen, dan moet je eerst twee van de drie vectoren uitkiezen om op te tellen, bijvoorbeeld de eerste en de tweede, en daarna het resultaat hiervan bij de derde vector optellen. Associativiteit vertelt je dan dat het niet uitmaakt met welke twee vectoren je begint.

In de praktijk zullen we haakjes doorgaans weglaten tenzij dat voor de context van belang is, bijvoorbeeld in een redenering. Hier is een voorbeeld met haakjes.
\[\vec{v}_1 + ((\vec{v}_2 + \vec{v}_3) + \vec{v}_4)\]
Dit lees je als volgt: tel eerst #\vec{v}_2# en #\vec{v}_3# op, tel het resultaat hiervan op bij #\vec{v}_4#, en tel ten slotte #\vec{v}_1# bij het resultaat van deze laatste berekening.

Commutativiteit

Bij het optellen van twee of meer vectoren kunnen we commutativiteit gebruiken om de volgorde van de termen naar eigen inzicht veranderen. Dat kan erg handig zijn bij berekeningen.

Aftrekking

De aftrekking is in het algemeen de operatie die optelling tenietdoet. Als we eerst #\vec{w}# bij #\vec{v}# optellen en vervolgens #\vec{w}# van het resultaat afrekken, krijgen we, dankzij de associativiteit, #\vec{v}# weer terug:

\[\left(\vec{v}+\vec{w}\right)-\vec{w} = \vec{v}+\left(\vec{w}-\vec{w}\right) =\vec{v}+\vec{0}=\vec{v}\]

Er zijn ook rekenregels waarin scalaire vermenigvuldiging en optelling beide een rol spelen.

Rekenregels voor scalaire vermenigvuldiging en optelling van vectoren

De scalaire vermenigvuldiging kent de volgende distributiviteitsregels.

Distributiviteit van de scalaire vermenigvuldiging over de vectoroptelling: #\lambda\cdot (\vec{v}+\vec{w}) = \lambda \cdot\vec{v} + \lambda \cdot\vec{w}# voor alle vectoren #\vec{v}#, #\vec{w}# en voor alle scalairen #\lambda#.
Distributiviteit van de scalaire vermenigvuldiging over de scalaire optelling:#(\lambda +\mu )\cdot\vec{v} = \lambda \cdot\vec{v}+\mu \cdot\vec{v}# voor alle scalairen #\lambda#, #\mu# en alle vectoren #\vec{v}#.

Beide uitspraken kunnen meetkundig bewezen worden. De bewijzen voor beide uitspraken volgen ook eenvoudig uit het uitschrijven van de uitdrukkingen in coördinaten en het toepassen van de uitdrukkingen voor de scalaire vermenigvuldiging en optelling van vectoren in termen van coördinaten.

Met gebruik van de aftrekking kunnen we elke vector in de vlak en ruimte in coördinaten beschrijven.

Vectoren in coördinaten

Als #P# en #Q# punten zijn van #\mathbb{R}^3# (of van #\mathbb{R}^2#), dan valt de vector #\vec{PQ}# samen met de vector van de oorsprong naar het punt #Q-P#. In termen van vectoren: \[\vec{PQ}=\vec{OQ}-\vec{OP}\]

Eerst bewijzen we de gelijkheid. De vector #\vec{PQ}# wordt verkregen door #\vec{OQ}# bij de vector #\vec{OP}# op te tellen. Dus #\vec{OP}+\vec{PQ}=\vec{OQ}#. Met behulp van deze gelijkheid vinden we \[\begin{array}{rcl}\vec{PQ}&=&\vec{PQ}+(1-1)\cdot\vec{OP}\\&&\phantom{xx}\color{blue}{0\cdot\vec{w}=\vec{0}\text{ en } \vec{v}+\vec{0}=\vec{v}}\\&=&\vec{PQ}+\vec{OP}-\vec{OP}\\&&\phantom{xx}\color{blue}{\text{ distributiviteit: }(1-1)\cdot\vec{w}=\vec{w}-\vec{w}}\\&=&\vec{OP}+\vec{PQ}-\vec{OP}\\&&\phantom{xx}\color{blue}{\text{commutativiteit}}\\&=&\vec{OQ}-\vec{OP}\end{array}\]

Interpreteren we de vectoren uit de gelijkheid in termen van coördinaten, dan zien we dat de coördinatenvector van de vector #\vec{PQ}# het verschil van de coördinatenvectoren van #Q# met #P# is. Vandaar de eerste uitspraak.

Wat is de som van de vectoren #\vec{v}=\rv{-29,-14,12}# en #\vec{w}=\rv{14,-1,-8}#?

#\rv{-15,-15,4}#

Elke coördinaat van de som #\vec{v}+\vec{w}# is de som van dezelfde coördinaten van #\vec{v}# en #\vec{w}#:
\[\begin{array}{rclcl}\vec{v}+\vec{w}&=&\rv{-29,-14,12}+\rv{14,-1,-8}&\phantom{x}&\color{blue}{\text{definities }\vec{v}, \vec{w}}\\ &=&\rv{-29+14,-14-1,12-8}&\phantom{x}&\color{blue}{\text{optelling per coördinaat}}\\&=&\rv{-15,-15,4}&\phantom{x}&\color{blue}{\text{vereenvoudigd}}\end{array}\]

In de figuur hieronder is de somvector getekend met een gestippelde pijl. De representant van de vector #\vec{v}# met beginpunt #\vec{w}# en de representant van de vector #\vec{w}# met beginpunt #\vec{v}# zijn blauw gestippeld.

Nieuw voorbeeld