Vector calculus in plane and space: Vectors in Planes and Space
 Linear combinations of vectors
Linear combinations of vectors
Scalar multiplications and additions of vectors can be combined as follows.
Linear combinations of vectors
If #\vec{v}_1# , #\vec{v}_2, \ldots , \vec{v}_n# is a list of #n# vectors and #\lambda_1#, #\lambda_2, \ldots, \lambda_n# are real numbers, then
\[
\lambda_1 \cdot\vec{v}_1 + \lambda_2\cdot \vec{v}_2 + \cdots + \lambda_n\cdot \vec{v}_n
\]
is called a linear combination of the vectors #\vec{v}_1#, #\vec{v}_2, \ldots, \vec{v}_n#.
The term linear combination is used to give a name to vectors that we can construct from a given set of vectors using the two operations vector addition and scalar multiplication.
Calculating with vectors is relatively easy. Thanks to the associativity and distributivity, you can often skip a lot of formal steps when calculating.
We cannot simply multiply vectors. There is, however, an operation for vectors in the space, the cross product, which shares some of the properties related to the conventional multiplication of numbers.
This follows from the following calculation:
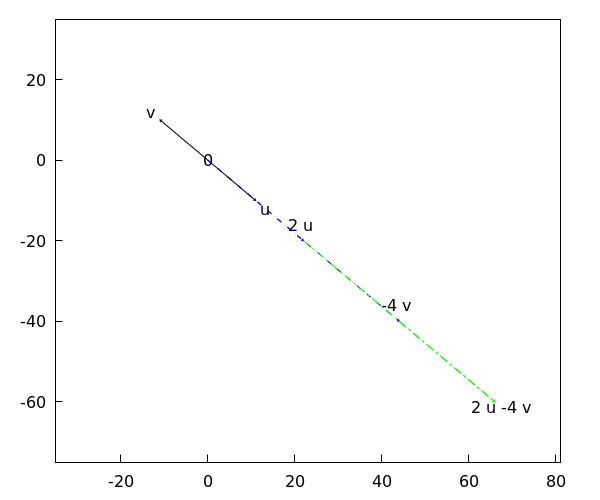
\[\begin{array}{rcl} 2\cdot\vec{u}-4\cdot\vec{v}&=&2\cdot\rv{11,-10}-4\cdot\rv{-11,10}\\
&&\qquad \blue{\text{definitions of }\vec{u}, \vec{v}}\\
&=&\rv{2\cdot 11, 2\cdot -10}+\rv{-4\cdot-11, -4\cdot 10}\\
&&\qquad \blue{\text{multiplication per coordinate}}\\
&=&\rv{22, -20}+\rv{44, -40}\\
&&\qquad \blue{\text{simplified}}\\
&=&\rv{22+44, -20-40}\\
&&\qquad \blue{\text{addition per coordinate}}\\
&=&\rv{66,-60}\\
&&\qquad \blue{\text{simplified}}\end{array}\]
The figure below shows the vectors #\vec{u}# and #\vec{v}# drawn in black, the vectors #2\cdot \vec{u}# and #-4\cdot\vec{v}# in blue dashed lines, and the vector #2\cdot\vec{u}-4\cdot\vec{v}# in a red dotted line.

Or visit omptest.org if jou are taking an OMPT exam.



