Straight lines in the plane in coordinates

Vector calculus in plane and space: Bases, Coordinates and Equations

Straight lines in the plane in coordinates

Once we have fixed coordinates, we can calculate in #\mathbb{R}^2#. This allows us to use the coordinates, often indicated by #x# and #y#. In particular, we are able to describe a straight line by means of a linear equation.

Let #\ell# be a straight line in the coordinate plane #\mathbb{R}^2# with position vector #\rv{a, b}# and direction vector #\rv{u, v}#. In addition to the parametric representation of the straight line:
\[\rv{x, y} = \rv{a, b}+ \lambda\cdot\rv{ u, v}\] #\ell# can also be described as the set of solutions #\rv{x,y}# of the equation \[v\cdot x - u\cdot y = v\cdot a - u\cdot b\]

Let #m# be the set of solutions #\rv{x,y}# for the equation #v\cdot x - u\cdot y = v\cdot a - u\cdot b#. We must demonstrate that #\ell# and #m# coincide.

For each value of #\lambda#, #\rv{x, y} =\rv{a, b}+ \lambda\cdot\rv{ u, v}# is a solution of this equation. After all, in this situation #x=a+\lambda\cdot u# and #y=b+\lambda\cdot v# apply, so \[\begin{array}{rcl}v\cdot x - u\cdot y &=& v\cdot \left(a+\lambda\cdot u \right) - u\cdot \left(b+\lambda\cdot v \right)\\&=&v\cdot a+ v\cdot u\cdot\lambda-u\cdot b-u\cdot v\cdot\lambda\\&=&v\cdot a-u\cdot b\\ \end{array}\] This proves that each point of #\ell# belongs to #m#.

We still have to show that each point of #m# belongs to #\ell#. In order to do so, we use the fact that #m# is a line. This is true because #\rv{u,v}# is a direction vector, so not equal to #\rv{0,0}#. This means #u\ne0# or #v\ne0#. If #u\ne0#, the equation of #m# can be written as \[y=\frac{v}{u}x-\frac{v\cdot a - u\cdot b}{u}\] and if #v\ne0#, the equation can be written as \[x= \frac{u}{v}\cdot y + \frac{v\cdot a - u\cdot b}{v}\] We can regard the equation as a parametric representation in both cases: \[\rv{x,y} =\begin{cases}\rv{0,\frac{ u\cdot b-v\cdot a}{u}}+x\cdot\rv{1,\frac{v}{u}}&\text{ if } u\ne0\\\rv{\frac{v\cdot a - u\cdot b}{v},0}+y\cdot\rv{\frac{u}{v},1}&\text{ if }v\ne0\end{cases}\] The solutions of the equation can be given in the parametric representation of a line, and, therefore, forms a line. Because the line #m# contains the line #\ell#, they must be equal. This proves the statement.

Sometimes, vectors are also described in columns. The parametric representation of #\ell# looks like this:
\[
\left(\begin{array}{l}
x \\ y
\end{array}\right)
=
\left(\begin{array}{l}
a \\ b
\end{array}\right)
+
\lambda
\left(\begin{array}{l}
u \\ v
\end{array}\right)
\] We will discuss this at a later point.

Often, we write #\rv{x_1,x_2}# instead of #\rv{x,y}#. Similarly, #\rv{a_1,a_2}# instead of #\rv{a,b}#, and #\rv{v_1,v_2}# instead of #\rv{u,v}#. This notation is consistent with the notation for higher dimensions.

Of course we can simply write: #x = a + \lambda\cdot u# and #y = b + \lambda\cdot v#. By eliminating #\lambda# from these two relations, we find an equation of the straight line: multiply #x = a + \lambda \cdot u# by #v#, and #y = b + \lambda\cdot v# by #u#, and subtract: \[v\cdot x - u\cdot y = v\cdot a - u\cdot b\]
a linear equation with unknown #x# and #y#.

Equations of straight lines are not unique, nor are parametric representations. For example, if you multiply an equation by 2, the result describes the same straight line.

A parametric representation of a straight line explicitly describes vectors/points of a straight: you can find a vector/point on the line (or its coordinates) for each #\lambda#. An equation of a straight line implicitly describes the straight line: #\rv{y_1, y_2}# is then and only then on the line if the coordinates satisfy the equation.

Does the segment #AB#, where #A = \rv{31,27}# and #B = \rv{91,81}#, intersect the line #l# given by the equation #5 x -9 y +26=0#?

no

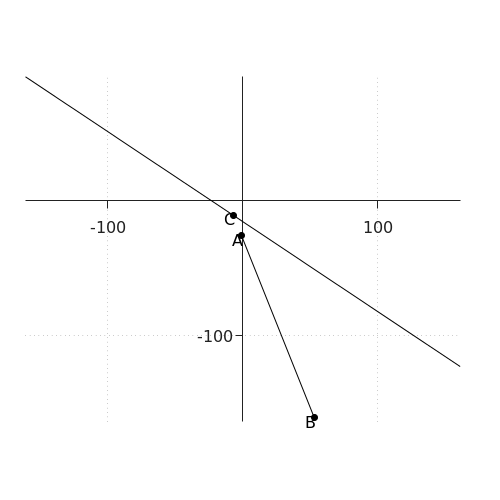
The line #A# and #B# has parametric representation #A+\lambda\cdot (B-A)#. If we enter the coordinates, we see \[\rv{31,27}+\lambda\cdot\rv{91-31,81-27}=\rv{31+60\lambda,27+54\lambda}\tiny.\] To see whether it includes a point of the line #l# given by equation #5 x -9 y +26=0#, we enter these coordinates for variables #x# and #y# in the equation \[\begin{array}{rclcl} 5( 31+60\lambda)-9 (27+54\lambda) +26 &=& 0 &\phantom{x}&\color{blue}{\text{coordinates entered}}\\ -62-186\lambda &=& 0 &\phantom{x}&\color{blue}{\text{simplified}}\\ \lambda &=& -{{1}\over{3}} &\phantom{x}&\color{blue}{\text{solved}}\\ \end{array} \] Because the value of #\lambda# not is between #0# and #1#, the intersection #A-{{1}\over{3}} \cdot (B-A)# does not belong to the segment #AB#. Hence, the answer is no. See the figure below.

There is actually another way to find out whether the line #l# intersects the segment #AB#: calculate the value of #5 x -9 y +26# for #\rv{x,y} = A# and of #\rv{x,y}=B#. If the two values have the not equal sign, then the line does intersect #AB#, otherwise, it does not. The explanation is that all points #\rv{x,y}# with #5 x -9 y +26\gt 0 # are on one side of #l#, and all points with #5 x -9 y +26\lt 0 # are on the other side. The value of #5 x -9 y +26# for #A# is #-62#, and the value for #B# is #-248#.

New example