Proof: Let $\varphi$ be the angle between $\vec{u}$ and $\vec{v}$.

1. If we take $\vec{u}$ for $\vec{v}$, the shared angle is $0^\circ$, which results in the fact that the cosine equals $1$, so $\vec{u}\cdot \vec{u} = \parallel\vec{u}\parallel^2$ . So

$$\parallel\vec{u}\parallel = \sqrt{\vec{u}\cdot \vec{u}}\tiny.$$ Note that in any case the dot product is equal to $0$ if one of the two vectors is the zero vector. The zero vector is orthogonal to each vector (the zero vector does not have a direction, but this is a convenient agreement).

2. The dot product $\vec{u}\cdot \vec{u}$ is the square of the length of the vector $\vec{u}$ because of 1, and thus not negative. If the dot product is equal to $0$ , then $\vec{u}$ is a vector of length $0$, and therefore must be the zero vector.

3. The angle between $\vec{v}$ and $\vec{u}$ is $-\varphi$, so the following applies

$$\vec{v}\cdot\vec{u} = \parallel \vec{v}\parallel\cdot\parallel\vec{u}\parallel\cdot\cos(-\varphi) = \parallel \vec{u}\parallel\cdot\parallel\vec{v}\parallel\cdot\cos(\varphi) = \vec{u}\cdot\vec{v}\tiny.$$

4. If $\lambda=0$ all elements equal $0$ and we are done with the proof. Assume, therefore, that $\lambda$ is not equal to $0$. The angle between $\vec{u}$ and $\lambda\cdot\vec{v}$ is equal to $\varphi$ if $\lambda\gt0$, and equal to $180^\circ-\varphi$ if $\lambda\lt0$. Consequently,

$$\vec{u}\cdot\left(\lambda\cdot\vec{v}\right) = \parallel\vec{u}\parallel\cdot\parallel\lambda\cdot\vec{v}\parallel\cdot\cos(\varphi)=\lambda\cdot\left(\vec{u}\cdot\vec{v}\right)$$ as $\lambda\gt0$ and $$\begin{array}{rcl}\vec{u}\cdot\left(\lambda\cdot\vec{v}\right) &=& \parallel\vec{u}\parallel\cdot\parallel\lambda\cdot\vec{v}\parallel\cdot\cos(180^\circ-\varphi)\\ &=&\left|\lambda\right|\cdot\parallel\vec{u}\parallel\cdot\parallel\vec{v}\parallel\cdot\left(-\cos(\varphi)\right)\\ &=&\lambda\cdot\parallel\vec{u}\parallel\cdot\parallel\vec{v}\parallel\cdot\cos(\varphi)\\ &=&\lambda\cdot\left(\vec{u}\cdot\vec{v}\right)\end{array}$$ as $\lambda\lt0$.

We conclude that, in all cases $\vec{u}\cdot\left(\lambda\cdot\vec{v}\right) = \lambda\cdot\left(\vec{u}\cdot\vec{v}\right)$ applies. The other equality can be proven in the same way.

5. We start with the first of the first two equations: $\vec{u}\cdot(\vec{v}+\vec{w}) = (\vec{u}\cdot \vec{v}) + (\vec{u}\cdot \vec{w})$. If $\vec{u}=\vec{0}$, the equality is true, because all terms are equal $0$. Therefore, we may assume that this is not true, so $\parallel\vec{u}\parallel\ne0$ and there is a unique line through the origin and $\vec{u}$. Call that line $\ell$.

It is sufficient to prove the equality in the case that $\parallel\vec{u}\parallel=1$. The general case then follows from the previous rule with $\lambda=\parallel\vec{u}\parallel$ :

$$\begin{array}{rcl}\vec{u}\cdot(\vec{v} + \vec{w}) &=&\lambda\cdot \left(\left(\frac{1}{\lambda}\cdot \vec{u}\right)\cdot(\vec{v} + \vec{w})\right)\\&=&\lambda\cdot\left(\left(\frac{1}{\lambda}\cdot \vec{u}\right)\cdot\vec{v} +\left(\frac{1}{\lambda}\cdot \vec{u}\right)\cdot\vec{w}\right)\\&=&\lambda\cdot\left(\frac{1}{\lambda}\cdot \vec{u}\right)\cdot\vec{v} +\lambda\cdot\left(\frac{1}{\lambda}\cdot \vec{u}\right)\cdot\vec{w}\\&=&\left( \vec{u}\cdot\vec{v}\right) +\left(\vec{u}\cdot\vec{w}\right)\\\end{array}$$ Note that $\parallel\frac{1}{\lambda}\cdot \vec{u}\parallel = \frac{1}{\lambda}\cdot\parallel\vec{u}\parallel=\frac{1}{\lambda}\cdot\lambda = 1$, so that in the case above, only the specific case with a vector of a length $1$ was used.

It is sufficient to prove the first equality as $\parallel\vec{u}\parallel=1$. In this case, because of The dot product, in terms of lengths, $(\vec{u}\cdot\vec{y})\cdot \vec{u}$ is the projection of $\vec{y}$ on $\ell$ for each vector $\vec{y}$. Let $A$ be the endpoint of $\vec{v}$, $B$ be the endpoint of $\vec{w}$, and $C$ be the endpoint of $\vec{v}+\vec{w}$, all three placed at the origin. Give the projection of respectively $A$, $B$, and $C$ on $\ell$ with $P_A$, $P_B$, and $P_C$. In that case $(\vec{u}\cdot\vec{v})\cdot \vec{u}=\vec{OP_A}$ , $(\vec{u}\cdot\vec{w})\cdot \vec{u}=\vec{OP_B}$ and $\left(\vec{u}\cdot(\vec{v}+\vec{w})\right)\cdot \vec{u}=\vec{OP_C}$. The equality that we want to prove follows if we can demonstrate that $\vec{OP_A}+\vec{OP_B}=\vec{OP_C}$. See the figure below.

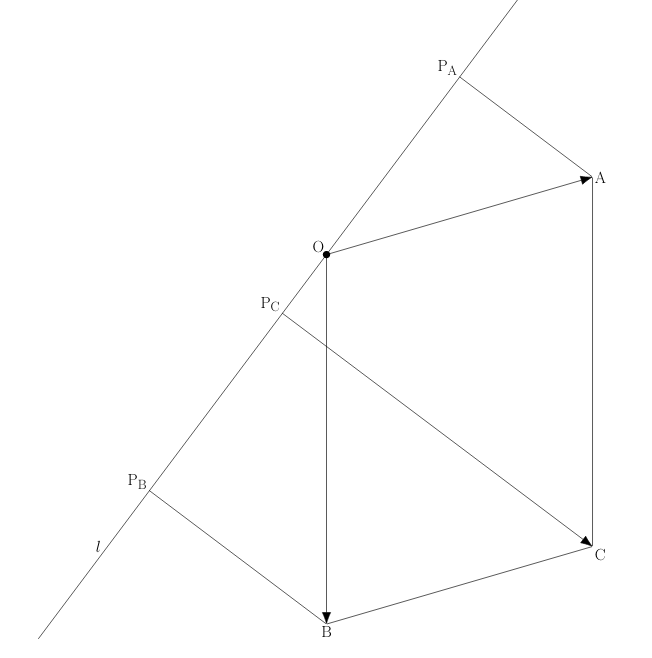
We will once more apply The dot product in terms of lengths, but now to the vector $\vec{v}$ and the line $\ell$, which comprises all the scalar multiples of $\vec{u}$. In that case $\vec{P_BP_C}$ is the projection of the vector $\vec{v}$, placed in $B$, onto $\ell$, so that $\vec{P_BP_C}=\vec{OP_A}$. Adding $\vec{OP_B}$ on both sides gives $\vec{OP_C}=\vec{OP_A}+\vec{OP_B}$, which proves the requested equality.

The second equality follows from the first when applying the third rule:

$$\begin{array}{rcl}(\vec{v}+\vec{w})\cdot\vec{u} &=&\vec{u}\cdot(\vec{v}+\vec{w})\\ &&\phantom{xxx}\color{blue}{\text{symmetry}}\\&=&(\vec{u}\cdot \vec{v})+(\vec{u}\cdot \vec{w})\\ &&\phantom{xxx}\color{blue}{\text{the first equality}}\\&=&(\vec{v}\cdot\vec{u})+(\vec{w}\cdot\vec{u})\\ &&\phantom{xxx}\color{blue}{\text{symmetry}}\end{array}$$

6. If $\vec{u}\cdot\vec{v}=0$, then $\parallel \vec{u}\parallel \cdot\parallel \vec{v}\parallel \cdot\cos(\varphi)=0$ applies, which means there are three cases to identify:

• $\parallel \vec{u}\parallel =0$: which means that $\vec{u}=0$, in which case $\vec{u}$ is, by definition, perpendicular to $\vec{v}$;
• $\parallel \vec{v}\parallel =0$: which means that $\vec{v}=0$, in which case $\vec{v}$ is, by definition, perpendicular to $\vec{u}$;
• $\cos(\varphi)=0$: which means that $\varphi=\pm\frac{\pi}{2}$, that is to say: $\vec{u}$ is perpendicular to $\vec{v}$.

The other implication (if $\vec{u}$ and $\vec{v}$ are mutually perpendicular, then $\vec{u}\cdot\vec{v}=0$ applies) can be proven by reversing the arguments above.