Laat $\varphi$ de hoek tussen $\vec{u}$ en $\vec{v}$ zijn.

1. Nemen we voor $\vec{v}$ ook $\vec{u}$, dan is de onderlinge hoek $0^\circ$, met als gevolg dat de cosinus gelijk aan $1$ is, zodat $\vec{u}\cdot \vec{u} = \parallel\vec{u}\parallel^2$. Dus

$$\parallel\vec{u}\parallel = \sqrt{\vec{u}\cdot \vec{u}}\tiny.$$ Merk op dat het inproduct sowieso gelijk aan $0$ is als een van beide vectoren de nulvector is. De nulvector staat loodrecht op elke vector (de nulvector heeft geen richting, maar dit is een handige afspraak).

2. Het inproduct $\vec{u}\cdot \vec{u}$ is vanwege 1. het kwadraat van de lengte van de vector $\vec{u}$ en dus niet-negatief. Als dit inproduct gelijk is aan $0$, dan is $\vec{u}$ een vector met lengte $0$, en moet daarom wel de nulvector zijn.

3. De hoek tussen $\vec{v}$ en $\vec{u}$ is $-\varphi$, dus geldt

$$\vec{v}\cdot\vec{u} = \parallel \vec{v}\parallel\cdot\parallel\vec{u}\parallel\cdot\cos(-\varphi) = \parallel \vec{u}\parallel\cdot\parallel\vec{v}\parallel\cdot\cos(\varphi) = \vec{u}\cdot\vec{v}$$

4. Als $\lambda=0$ dan zijn alle onderdelen gelijk aan $0$ en zijn we klaar met het bewijs. Veronderstel daarom dat $\lambda$ niet gelijk aan $0$ is. De hoek tussen $\vec{u}$ en $\lambda\cdot\vec{v}$ is gelijk aan $\varphi$ als $\lambda\gt0$ en gelijk aan $180^\circ-\varphi$ als $\lambda\lt0$. Bijgevolg is

$$\vec{u}\cdot\left(\lambda\cdot\vec{v}\right) = \parallel\vec{u}\parallel\cdot\parallel\lambda\cdot\vec{v}\parallel\cdot\cos(\varphi)=\lambda\cdot\left(\vec{u}\cdot\vec{v}\right)$$ als $\lambda\gt0$ en $$\begin{array}{rcl}\vec{u}\cdot\left(\lambda\cdot\vec{v}\right) &=& \parallel\vec{u}\parallel\cdot\parallel\lambda\cdot\vec{v}\parallel\cdot\cos(180^\circ-\varphi)\\ &=&\left|\lambda\right|\cdot\parallel\vec{u}\parallel\cdot\parallel\vec{v}\parallel\cdot\left(-\cos(\varphi)\right)\\ &=&\lambda\cdot\parallel\vec{u}\parallel\cdot\parallel\vec{v}\parallel\cdot\cos(\varphi)\\ &=&\lambda\cdot\left(\vec{u}\cdot\vec{v}\right)\end{array}$$ als $\lambda\lt0$.

We concluderen dat, in alle gevallen $\vec{u}\cdot\left(\lambda\cdot\vec{v}\right) = \lambda\cdot\left(\vec{u}\cdot\vec{v}\right)$ geldt. De andere gelijkheid kan net zo bewezen worden.

5. We concentreren ons eerst op de eerste van de twee gelijkheden: $\vec{u}\cdot(\vec{v}+\vec{w}) = (\vec{u}\cdot \vec{v}) + (\vec{u}\cdot \vec{w})$. Als $\vec{u}=\vec{0}$, dan is de gelijkheid waar omdat alle termen gelijk zijn aan $0$. Daarom mogen we veronderstellen dat dit niet zo is, zodat $\parallel\vec{u}\parallel\ne0$ en er een unieke lijn door de oorsprong en $\vec{u}$ gaat. Noem die lijn $\ell$.

Het is voldoende de gelijkheid te bewijzen voor het geval dat $\parallel\vec{u}\parallel=1$. Want het algemene geval volgt dan uit de voorgaande regel met $\lambda=\parallel\vec{u}\parallel$:

$$\begin{array}{rcl}\vec{u}\cdot(\vec{v} + \vec{w}) &=&\lambda\cdot \left(\left(\frac{1}{\lambda}\cdot \vec{u}\right)\cdot(\vec{v} + \vec{w})\right)\\ &&\phantom{xx}\color{blue}{\text{gemengde associativiteit}}\\&=&\lambda\cdot\left(\left(\frac{1}{\lambda}\cdot \vec{u}\right)\cdot\vec{v} +\left(\frac{1}{\lambda}\cdot \vec{u}\right)\cdot\vec{w}\right)\\&&\phantom{xx}\color{blue}{\parallel{\frac{1}{\lambda}}\cdot \vec{u}\parallel = 1}\\&=&\lambda\cdot\left(\left(\frac{1}{\lambda}\cdot \vec{u}\right)\cdot\vec{v}\right) +\lambda\cdot\left(\left(\frac{1}{\lambda}\cdot \vec{u}\right)\cdot\vec{w}\right)\\&&\phantom{xx}\color{blue}{\text{distributiviteit voor reële getallen}}\\&=&\left( \vec{u}\cdot\vec{v}\right) +\left(\vec{u}\cdot\vec{w}\right)\\&&\phantom{xx}\color{blue}{\text{gemengde associativiteit}}\\ \end{array}$$ Merk op dat $\parallel\frac{1}{\lambda}\cdot \vec{u}\parallel = \frac{1}{\lambda}\cdot\parallel\vec{u}\parallel=\frac{1}{\lambda}\cdot\lambda = 1$, zodat in bovenstaande inderdaad alleen het speciale geval van een vector met lengte $1$ gebruikt is.

Het is dus voldoende de eerste gelijkheid te bewijzen als $\parallel\vec{u}\parallel=1$. In dit geval is voor elke vector $\vec{y}$, vanwege Het inproduct in termen van lengtes, $(\vec{u}\cdot\vec{y})\cdot \vec{u}$ de projectie van $\vec{y}$ op $\ell$. Laat $A$ het eindpunt van $\vec{v}$ zijn, $B$ het eindpunt van $\vec{w}$, en $C$ het eindpunt van $\vec{v}+\vec{w}$, alledrie geplaatst in de oorsprong. Geef met $P_A$, $P_B$ en $P_C$ de projectie van respectievelijk $A$, $B$ en $C$ op $\ell$ aan. Dan is $(\vec{u}\cdot\vec{v})\cdot \vec{u}=\vec{OP_A}$, $(\vec{u}\cdot\vec{w})\cdot \vec{u}=\vec{OP_B}$ en $\left(\vec{u}\cdot(\vec{v}+\vec{w})\right)\cdot \vec{u}=\vec{OP_C}$. De gelijkheid die we willen bewijzen volgt dus als we kunnen laten zien dat $\vec{OP_A}+\vec{OP_B}=\vec{OP_C}$. Zie onderstaande figuur.

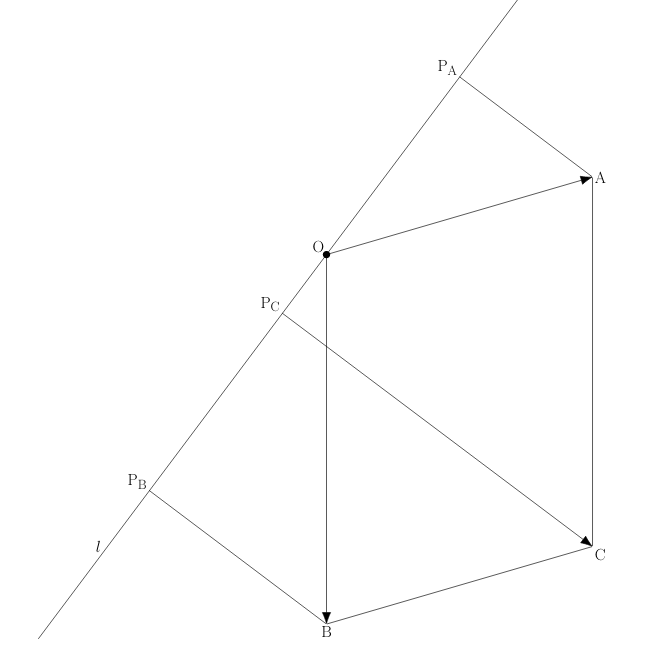
We passen nogmaals Het inproduct in termen van lengtes toe, maar nu op de vector $\vec{v}$ en de lijn $\ell$ die bestaat uit alle scalaire veelvouden van $\vec{u}$. Dan is $\vec{P_BP_C}$ de projectie van de vector $\vec{v}$, geplaatst in $B$, op $\ell$, zodat $\vec{P_BP_C}=\vec{OP_A}$. Optellen van $\vec{OP_B}$ aan beide zijden geeft $\vec{OP_C}=\vec{OP_A}+\vec{OP_B}$, wat de gevraagde gelijkheid bewijst.

De tweede gelijkheid volgt uit de eerste door toepassing van de derde regel:

$$\begin{array}{rcl}(\vec{v}+\vec{w})\cdot\vec{u} &=&\vec{u}\cdot(\vec{v}+\vec{w})\\ &&\phantom{xxx}\color{blue}{\text{symmetrie}}\\&=&(\vec{u}\cdot \vec{v})+(\vec{u}\cdot \vec{w})\\ &&\phantom{xxx}\color{blue}{\text{de eerste gelijkheid}}\\&=&(\vec{v}\cdot\vec{u})+(\vec{w}\cdot\vec{u})\\ &&\phantom{xxx}\color{blue}{\text{symmetrie}}\end{array}$$

6. Als $\vec{u}\cdot\vec{v}=0$, dan geldt $\parallel \vec{u}\parallel \cdot\parallel \vec{v}\parallel \cdot\cos(\varphi)=0$, dus zijn er drie gevallen die we onderscheiden:

• $\parallel \vec{u}\parallel =0$: dit betekent dat $\vec{u}=0$, in welk geval $\vec{u}$ per definitie loodrecht op $\vec{v}$ staat;
• $\parallel \vec{v}\parallel =0$: dit betekent dat $\vec{v}=0$, in welk geval $\vec{v}$ per definitie loodrecht op $\vec{u}$ staat;
• $\cos(\varphi)=0$: dit betekent dat $\varphi=\pm\frac{\pi}{2}$, dat wil zeggen: $\vec{u}$ staat loodrecht op $\vec{v}$.

De andere implicatie (als $\vec{u}$ en $\vec{v}$ onderling loodrecht zijn, dan geldt $\vec{u}\cdot\vec{v}=0$) is te bewijzen door bovenstaande redeneringen om te draaien.