Kansverdelingen

Hoofdstuk 4: Kansverdelingen: Kansvariabelen

Kansverdelingen

Kansverdeling

Definitie

Een kansverdeling is een functie die elke uitkomst van een kansexperiment koppelt aan de kans dat de uitkomst zich voordoet.

Notatie

De kansverdeling van een kansvariabele #X# wordt aangeduid met #f(x)#.

#\phantom{0}#

KansfunctieDe kansverdeling van een discrete kansvariabele wordt een kansfunctie genoemd.

Een kansfunctie geeft, voor elke waarde #x# die de kansvariabele kan aannemen, de kans dat #X# gelijk is aan #x#.
\[f(x)=\mathbb{P}(X=x)\]

De cumulatieve verdelingsfunctie van een discrete kansvariabele geeft de kans aan dat #X# kleiner dan of gelijk is aan #x#.

\[F(x)=\mathbb{P}(X\leq x)\]

Stel je een kansexperiment voor waarbij we twee keer een muntje opgooien. Laat #X# het aantal keer zijn dat de munt met Kop bovenkomt.

Dan is de kansverdeling van #X#:

#x#	#0#	#1#	#2#
#\mathbb{P}(X=x)#	#0.25#	#0.5#	#0.25#

Rekenregels discrete kansverdeling

Voor elke discrete kansverdeling gelden de volgende rekenregels:

#\mathbb{P}(X \leq x) = \mathbb{P}(X=0) +\mathbb{P}(X=1) + \ldots + \mathbb{P}(X=x)#
#\mathbb{P}(X \geq x) = 1 - \mathbb{P}(X \lt x) = 1 - \mathbb{P}(X \leq x-1)#
#\mathbb{P}(X \lt x) = \mathbb{P}(X \leq x-1) = 1 - \mathbb{P}(X \geq x)#
#\mathbb{P}(X \gt x) = \mathbb{P}(X \geq x+1) = 1 - \mathbb{P}(X \leq x)#

Bovendien geldt voor elke #2# waarden #a# en #b# in het bereik van #X# (met #a<b# ) dat:

#\mathbb{P}(a \lt X \leq b) = \mathbb{P}(X \leq b) - \mathbb{P}(X \leq a)#

#\phantom{0}#

Kansdichtheidsfunctie
De kansverdeling van een continue kansvariabele wordt een kansdichtheidsfunctie genoemd.

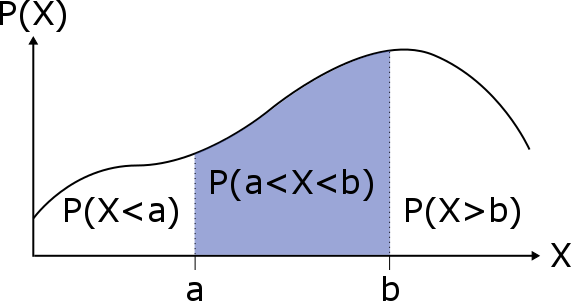
De kans dat een kansvariabele #X# tussen de punten #a# en #b# valt is gelijk aan het oppervlakte onder de curve tussen #a# en #b#.
#\phantom{0}#

Rekenregels continue kansverdeling

Voor elke continue kansverdeling gelden de volgende rekenregels:

#\mathbb{P}(X=k)=0#
#\mathbb{P}(X\leq k)=\mathbb{P}(X\lt k) =1 - \mathbb{P}(X \geq k)#
#\mathbb{P}(X\geq k)=\mathbb{P}(X\gt k)= 1 - \mathbb{P}(X \leq k)#

Bovendien, voor elke #2# waarden #j# en #k# (met #j\lt k# ), gelden de volgende rekenregels:

#\mathbb{P}(j\lt X\lt k)=\mathbb{P}(j\leq X \lt k)=\mathbb{P}(j \lt X\leq k)=\mathbb{P}(j\leq X\leq k)#
#\mathbb{P}(k\gt X \gt j)=\mathbb{P}(k\geq X \gt j)=\mathbb{P}(k\gt X\geq j)=\mathbb{P}(k \geq X\geq j)#
#\mathbb{P}(j \leq X \leq k) = \mathbb{P}(X \leq k) - \mathbb{P}(X \leq j)#