De normale verdeling

Hoofdstuk 4: Kansverdelingen: Veelvoorkomende continue kansverdelingen

De normale verdeling

De normale verdeling is misschien wel de belangrijkste verdeling in de statistiek. Het blijkt dat veel variabelen waarin we binnen de wetenschap in geïntereseerd zijn bij benadering normaal verdeeld zijn. Bij mensen zijn kenmerken zoals bijvoorbeeld lengte, gewicht, draagtijd, en intelligentie allemaal (ongeveer) normaal verdeeld.

De normale verdeling speelt ook een zeer belangrijke rol in de verklarende statistiek. Dit kom doordat veel technieken uit deze tak van de statistiek gebaseerd zijn op de aanname dat een variabele normaal verdeeld is.

Een normale verdeling is continu, symmetrisch, unimodaal, klokvormig en asymptotisch * ten opzichte van de horizontale as.

Het gemiddelde, de modus, en de mediaan van een normale verdeling vallen samen op hetzelfde punt in het midden van de verdeling.

De notatie voor een normale verdeling met een gemiddelde #\mu# en standaarddeviatie #\sigma# is: \[N(\mu, \sigma)\]

Asymptotisch

Asymptotisch betekent dat de curve van een normale verdeling steeds dichterbij de horizontale as komt naarmate de afstand tot het gemiddelde toeneemt, maar op enkel punt contact met de as maakt

#\phantom{0}#
De normale verdeling heeft de volgende formule:

\[f(x) = \dfrac{1}{\orange{\sigma} \sqrt{2\pi}}e^{-\dfrac{(x-\blue{\mu})^2}{2\orange{\sigma}^2}}\]

Het is gelukkig niet nodig om deze te formule te onhouden. Het belangrijkste om mee te nemen is dat er #2# variabelen zijn die de kenmerken van een normale verdeling bepalen, namelijk het gemiddelde #\blue{\mu}# en de standaarddeviatie #\orange{\sigma}# van de verdeling.

Het veranderen van #\blue{\mu}# verschuift de hele curve naar links of naar rechts. Een andere manier om hiernaar te kijken is dat de waarde van het gemiddelde de #\blue{\text{positie}}# van de verdeling langs de schaal bepaalt.
Het veranderen van #\orange{\sigma}# clustert ofwel de scores dichter bij elkaar of spreidt ze uit. Met andere woorden, de standaardafwijking bepaalt de #\orange{\text{vorm}}# van de normale verdeling.
#\phantom{0}#

Normale Verdeling Interactief

#\phantom{0}#

Oppervlakte onder de normale verdeling
Hoewel er veel verschillende normale verdelingen bestaan, hebben ze hebben allemaal de volgende eigenschappen met betrekking tot het oppervlakte onder de curve:

De totale oppervlakte onder een normale verdeling is gelijk aan #1#.
Het gebied aan de linkerkant van het gemiddelde is precies gelijk aan het gebied aan de rechterkant van het gemiddelde, namelijk #0.5#.
De empirische regel geldt.

Empirische regel
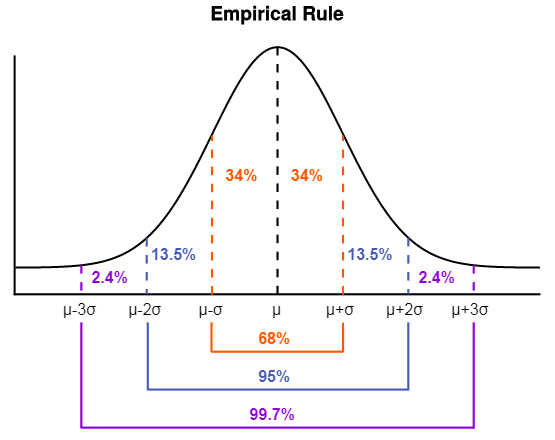
Als een verdeling van de scores normaal is verdeeld, dan kunnen we de empirische regel gebruiken om de volgende uitspraken te doen over de spreiding van de scores rondom het gemiddelde:

Ongeveer #68\%# van de scores liggen binnen 1 standaardafwijking van het gemiddelde #(\mu \pm 1\sigma)#.
Ongeveer #95\%# van de scores liggen binnen 2 standaardafwijkingen van het gemiddelde #(\mu \pm 2\sigma)#.
Ongeveer #99.7\%# van de scores liggen binnen 3 standaardafwijkingen van het gemiddelde #(\mu \pm 3\sigma)#.

\[\text{}\]

Standaard normale verdeling
De standaard normale verdeling is een normale verdeling met gemiddelde #\mu=0# en standaardafwijking #\sigma=1#.

Laat #X# een continue kansvariabele zijn. Als #X\sim N(\mu, \sigma)#, dan zijn de #Z#-scores die we op basis van #X# berekenen standaard normaal verdeeld:

\[Z=\cfrac{X-\mu}{\sigma}\sim N(0,1)\]